Einleitung
Um nach dem Flop die richtigen Entscheidungen treffen zu können, ist es unerlässlich, sich ein wenig mit dem Thema "odds und outs" auszukennen. Auch hier werde ich nicht all zu tief gehen, es geht mir hier nur darum, die mathematischen Grundlagen zu erklären.
draws
Tatsache ist, dass du nach dem Flop meist keine Hand hast, mit der du einen showdown gewinnen kannst. Das heisst aber noch lange nicht, dass all die schönen Hände gefoldet werden müssen, da sie in vielen Fällen das Potenzial haben, sich auf Turn oder River noch stark zu verbessern. Wenn eine reale Chance dazu besteht, spricht man von einem "draw". Die häufigsten, spielbaren draws sind der "flushdraw" und der "straightdraw".
Beispiel für einen
flushdraw:
Du hast
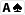
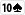
und nach dem Flop liegt
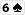
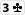
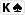
oder
du hast


und nach dem Turn liegt


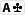

In beiden Fällen hast du 4 Karten zu einem Flush und brauchst eine weitere der Farbe, um ihn zu komplettieren.
Bei den straightdraws unterschiedet man zwischen "open endend straightdraws", "gutshot- oder belly-buster-straightdraws" und "double-belly-buster-straightdraws".
open-ended straightdraw
beim open-ended straightdraw hast du vier aufeinanderfolgende Karten. Die Bezeichnung "open-ended" sagt es eigentlich schon: Es kann am oberen oder unteren "Ende" der Reihe eine Karte kommen, welche die Strasse vollendet.
Beispiel:
Du hast
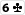
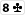
und nach dem Flop liegt


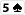
eine
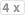
oder eine
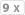
würden dir hier eine straight bescheren.
gutshot- oder belly-buster-straightdraws
Wenn du vier Karten einer straight hast, die in der Mitte eine Lücke aufweisen, dann spricht man von einem gutshot-straightdraw.
Beispiel:
Du hast
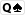

und nach dem Flop liegt
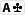
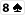

In diesem Fall hilft dir nur noch eine Karte zur straight, nämlich die
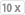
. Man spricht grundsätzlich von einem gutshot-straightdraw, wenn nur EINE Karte zur straight führt, selbst wenn die Lücke am anfang oder am Ende der Reihe liegt.
Beispiele dafür:
Du hast
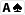
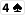
und nach dem Flop liegt

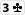
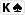
-> du brauchst eine
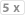
oder
du hast


und nach dem Flop liegt


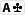
-> du brauchst eine
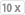 double-belly-buster-straightdraw
double-belly-buster-straightdraw
Der double-belly-buster-straightdraw ist nicht so einfach zu erkennen und wird häufig übersehen. Ist auch nicht ganz simpel zu erklären, doch ich versuchs mal so: Es handelt sich hier um 7 aufeinanderfolgende Karten, mit 2 Lücken. Eine an 2. und eine an 6. Stelle. Kapiert? Nicht? OK, dann so:
X = Karte
O = Lücke
Ein open-ended straightdraw würde so aussehen: OXXXXO,
ein gutshot-straightdraw so: XOXXX oder XXOXX oder XXXOX
und ein double-belly-buster-straightdraw so: XOXXXOX
Klingt furchtbar kompliziert, ein Beispiel sollte aber Klarheit schaffen:
Du hast


und nach dem Flop liegt

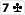
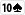
Wie bei dem open-ended-straightdraw hast du hier 2 Karten, die dir eine straight geben, nämlich eine
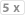
oder eine
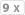
Es gibt natürlich noch mehr draws als die oben beschriebenen, aber für den Anfang sollte das genügen.
outs
Nicht alle draws sind gleich stark. Um die Stärke eines draws zu beschreiben, bedient man sich unter anderem des Begriffs "outs". Kurz und knackig: ein "out" ist eine Karte im Stapel, die mir, wenn sie auf Turn oder River erscheint, mit grosser Wahrscheinlichkeit die Gewinner-Hand einbringt. Je mehr outs ich habe, desto höher ist die Wahrscheinlichkeit, dass ich treffe.
Beispiel flushdraw:
Du hast
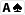
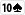
und nach dem Flop liegt
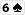
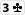
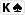
Wenn hier eine weitere Pik-Karte fällt, habe ich mit grosser Wahrscheinlichkeit beim showdown die beste Hand. Die Ausnahme wäre, wenn z.B. jemand
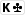

halten würde, und auf dem Turn die
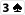
käme. Wir hätten dann den gewünschten flush, der Gegner hätte uns allerdings mit einem full house geschlagen. Der Einfachheit halber nehmen wir nun aber einfach an, ein flush genügt uns zum Sieg.
Also, noch einmal: Wir benötigen eine Pik-Karte zum Sieg. Im ganzen Deck sind 13 Pik-Karten. 2 davon halten wir in der Hand, 2 liegen auf dem board, macht 9 Pik-Karten, die der dealer noch aufdecken könnte. Wir haben also
9 outs.
Beispiel gutshot-straightdraw
Du hast
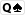

und nach dem Flop liegt
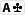
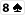

Wir benötigen eine
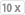
zum Sieg. Im ganzen Deck hat es 4
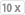
, keine liegt auf dem board, wir haben keine in der Hand, also haben wir hier
4 outs.
odds
Was nützt es mir nun, wenn ich einen flushdraw erkennen kann? Was ist jetzt mit den outs? Soll ich folden? Soll ich callen?
Hier kommt nun die Mathematik ins Spiel. Keine Angst, ich bin nur bedingt begabt auf diesem Terrain, doch sogar ich habe es begriffen. Kann also nicht allzu schwer sein.
Um mit einem flushdraw eine Bet zu callen, müssen die "odds" stimmen, damit es auf Dauer rentabel ist. "Odds" ist der englische Ausdruck für "Gewinnchanen". zur Erklärung: Wenn du beim Würfeln auf eine bestimmte Zahl setzt, dann sind deine odds 1/6, dass diese Zahl auch fällt. Wenn es um Poker geht, spricht man allerdings nicht von 1/6, sondern von 1:5 (im Schnitt 1 mal Treffer, 5 mal kein Treffer). So weit, so gut. Ein weiterer Begriff, den du kennen musst, ist "pot-odds".
Die pot-odds sind das Verhältnis von dem Betrag den du riskierst, zu dem Betrag, den du gewinnen kannst.
Ein kleines Bespiel:
Ich biete dir folgendes an: du setzt 5.- auf eine Zahl. Du würfelst. Wenn du die Zahl triffst, gebe ich dir den Einsatz plus 25.- . Um zu ermitteln, ob das für dich auf Dauer profitabel ist, musst du nun die "pot-odds" mit den "odds" vergleichen:
Einsatz: 5.-
Reingewinn bei einem Treffer: 25.-
Entsprich pot-odds von 5:25 oder 1:5
Die odds, dass du die Zahl triffst, sind wie oben ermittelt 1:5
Nun spielen wir das ganze mal durch und zwar sechs mal:
Im Schnitt wirst du 1mal gewinnen, macht
+25.-
Im Schnitt wirst du 5mal den Einsatz verlieren, macht
–25.-
Summe = 0
Du siehst, du kannst hier setzen und würfeln, bis du alt und grau bist, unter dem Strich wirst du nichts gewinnen und nichts verlieren.
Fazit: Sind die pot-odds gleich gross wie die odds, dann hast du eine +/-0 –Situation.
Nun erhöhe ich mein angebot auf 30.- bei einem Treffer. Die Situation sieht nun wie folgt aus:
pot-odds = 5:30 = 1:6
odds immer noch = 1:5
das ganze wieder 6 mal:
Im Schnitt wirst du 1mal gewinnen, macht
+30.-
Im Schnitt wirst du 5mal den Einsatz verlieren, macht
–25.-
Summe =
+5.-
Da wir hier 6 mal gewürfelt haben, beträgt dein Gewinn pro Wurf 5/6 = 0.83. Diese Spiel ist also rentabel für dich. Du machst mit jedem Wurf unter dem Strich einen Gewinn von
0.83.
Fazit: Sind die pot-odds höher als die odds, machst du auf Dauer Gewinn.
Der Vollständigkeit halber spielen wir das ganze noch einmal durch, diesmal mit einem Gewinn von 20.- pro Treffer.
pot-odds = 5:20 = 1:4
odds immer noch = 1:5
das ganze wieder 6 mal:
Im Schnitt wirst du 1mal gewinnen, macht
+20.-
Im Schnitt wirst du 5mal den Einsatz verlieren, macht
–25.-
Summe =
-5.-
Entspricht einem Verlust von
0.83 pro Wurf.
Fazit: Sind die pot-odds tiefer als die odds, machst du auf Dauer Verlust.
die Praxis
Dieses Vorgehen lässt sich nun 1:1 am Pokertisch anwenden. Die pot-odds sind schnell berechnet.
Beispiel:
Im Pot sind 40.-
ein Spieler vor dir setzt 10.-
du musst also 10.- callen um 50.- (40 schon im Pot, 10 vom Gegner) zu gewinnen -> pot-odds = 10:50 = 1:5
Für die Berechnung der odds brauchen wir nun die outs. Bei einem flushdraw hast du also 9 outs. Im ganzen Deck sind 52 Karten. 2 Hast du in der Hand, 3 liegen auf dem board, macht 47 unbekannte Karten. Wahrscheinlichkeit oder odds, dass eine deiner Karten kommt = 9/47 ist ungefähr gleich 1/5 und das entspricht odds von 1:4.
-> pot-odds (1:5) sind höher als odds (1:4) -> rentabel -> CALL
Das selbe Spiel noch einmal, nun mit dem gutshot-straightdraw:
pot-odds = 1:5
Anzahl outs = 4
odds = 4/47 ist ungefähr gleich 1/12 entspricht 1:11
-> pot-odds (1:5) sind tiefer als odds (1:11) -> unrentabel -> FOLD
Für das ganze Gerechne bleibt am Tisch und in der Hitze des Gefechts natürlich wenig Zeit. Deshalb rate ich dir, die wichtigsten Zahlen einfach auswendig zu lernen. Sind nicht viele, und wenn du sie regelmässig anwendest kannst du sie bald im Schlaf. Hier eine Tabelle:
![[Bild: oddstabelletz1.jpg]](http://img142.imageshack.us/img142/5837/oddstabelletz1.jpg)
Wenn du dieses Prinzip einmal begriffen hast und es auch anwendest, hast du dem Durchschnitts-Pokerspieler schon einiges voraus. Also studiere dieses Thema, bis du es wirklich verstanden hast.
unbrauchbare outs
Beim Zählen der outs werden häufig Fehler gemacht. Es werden oft Karten als outs gezählt, die dir zwar die gewünschte Hand einbringen, dem Gegner aber eine stärkere. Grundsätzlich sollten die outs eher pessimistisch berechnet werden.
Beispiel:
Du hast
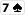
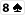
und nach dem Flop liegt
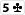
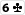

-> open ended straightdraw für dich.
Hier hast du ja 8 outs:

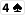

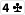

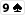

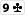
Streng gesehen darfst du hier die
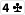
und die
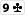
nicht als outs zählen, da sie jemandem mit einem flushdraw zu einer stärkeren Hand verhelfen. Bei nur einem Gegner ist das relativ unwahrscheinlich, bei mehreren Gegnern musst du fast davon ausgehen. Somit würden nur noch 6 outs übrigbleiben und deine odds sich signifikant verschlechtern.
Ein weiterer Fehler, der oft gemacht wird, ist das drawen zu einer straight oder einem flush, wenn bereits ein Pair auf dem board liegt. Sobald das der Fall ist, ist ein full house möglich und deine outs lösen sich unter Umständen allesamt in Luft auf.
Wenn du am drawen bist solltest du dir immer bildlich das board vorstellen, wie es aussieht, wenn du eins deiner outs triffst. Sind stärkere Hände möglich? Wenn ja, ist es realistisch, dass jemand diese Hand hält?
implied odds
Bis jetzt haben wir nur immer von pot-odds gesprochen. Wir sind davon ausgegangen, dass wir, wenn wir treffen, nur das gewinnen was im Pot ist. Doch wenn ich auf Turn oder River eins meiner outs treffe, habe ich immer noch die Chance, den Pot in den nächsten zwei Setzrunden "hochzutreiben". Die Summe, die ich erwarte noch rauskitzeln zu können, benötige ich für die Berechnung der "implied odds". So wird manchmal ein call gerechtfertigt, der nach pot-odds-Berechnung eigentlich ein klarer fold gewesen wäre. Das Problem dabei: Es basiert alles auf Annahmen, und diese werden meist viel zu optimistisch getroffen.
Beispiel:
Du hast einen As-flushdraw auf dem Flop. Im Pot sind zu diesem Zeitpunkt 20$. Dein Gegner spielt 10$ an. Pot-odds für dich: 1:3. Bei 1:4 odds für einen flushdraw ein klarer Fold. Um einen call zu rechtfertigen, sind 10$ zu wenig im Pot, was dir pot-odds von 1:4 geben würde. Nun musst die dir die alles entscheidende Frage stellen:
Ist es realistisch, dass ich – wenn ich den flush treffe – die 10$ des Gegners noch in den Pot kriege?
Diese Frage kann man hier und jetzt nicht beantworten, da sie im höchsten Masse vom Gegner abhängig ist. Spielt er aggressiv? Ist er aufmerksam? Spielt er ängstlich? usw.
Unabhänig vom Gegner wird die Höhe der implied odds auch von der Art der Hand beeinflusst. "versteckte" Hände haben viel höhere implied odds als solche, die sofort erkannt werden.
Beispiel:
Du hast
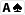
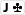
und nach dem Flop liegt
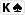
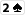
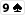
Hier hast du einen flushdraw, aber einen sehr offensichtlichen. Fällt eine weitere Pik-Karte, wird es nahezu unmöglich, hier noch Geld vom Gegner zu holen. Die implied odds sind bei diesen Beispiel praktisch gleich null.
nehmen wir mal das Beispiel des double-belly-buster-straightdraws:
Du hast


und nach dem Flop liegt

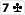
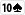
Hier kannst du schon wesentlich optimistischer zu Werke gehen. Selbst wenn du eins deiner outs triffst, sieht das board immer noch ziemlich harmlos aus und deine Chancen, von jemandem mit TopPair, TwoPair oder gar Trips ausgezahlt zu werden, stehen nicht schlecht.
Das wichtigste ist aber, dass du dich nicht selbst belügst, wenn du die implied odds berechnest. Ein call mit einem gutshot-straightdraw und pot-odds von 1:2 ist eigentlich fast immer falsch und sich einzureden, durch super-raffiniertes Spiel daraus 1:11 machen zu können ist Wunschdenken. Als Anfänger würde ich dir anraten, vorerst nur mit den pot-odds zu arbeiten, dann bist du immer auf der sicheren Seite.
Schlusswort
Auch bei diesem Thema kratze ich natürlich nur an der Oberfläche. Die Bücher in der
Liste von Grandmaster Flush und Paxinor enthalten wesentlich detailiertere Ausführungen zu diesem Thema.














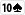 und nach dem Flop liegt
und nach dem Flop liegt 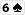
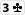
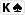

 und nach dem Turn liegt
und nach dem Turn liegt 

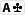

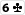
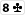 und nach dem Flop liegt
und nach dem Flop liegt 
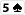
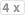 oder eine
oder eine 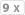 würden dir hier eine straight bescheren.
würden dir hier eine straight bescheren.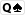
 und nach dem Flop liegt
und nach dem Flop liegt 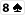

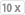 . Man spricht grundsätzlich von einem gutshot-straightdraw, wenn nur EINE Karte zur straight führt, selbst wenn die Lücke am anfang oder am Ende der Reihe liegt.
. Man spricht grundsätzlich von einem gutshot-straightdraw, wenn nur EINE Karte zur straight führt, selbst wenn die Lücke am anfang oder am Ende der Reihe liegt.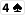 und nach dem Flop liegt
und nach dem Flop liegt 
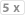


 und nach dem Flop liegt
und nach dem Flop liegt 
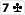
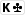
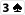 käme. Wir hätten dann den gewünschten flush, der Gegner hätte uns allerdings mit einem full house geschlagen. Der Einfachheit halber nehmen wir nun aber einfach an, ein flush genügt uns zum Sieg.
käme. Wir hätten dann den gewünschten flush, der Gegner hätte uns allerdings mit einem full house geschlagen. Der Einfachheit halber nehmen wir nun aber einfach an, ein flush genügt uns zum Sieg.![[Bild: oddstabelletz1.jpg]](http://img142.imageshack.us/img142/5837/oddstabelletz1.jpg)
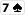
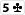

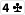
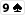
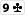
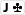 und nach dem Flop liegt
und nach dem Flop liegt 
![[Bild: pokersthumbsup.gif]](http://shiut555.googlepages.com/pokersthumbsup.gif)
